Combinational Design

Objectives


Examine the Combinational Design Procedure 
Review the Karnaugh Map Reduction Method
Build circuits to verify combinational design procedures

Logic elements like NAND and OR, which we looked at previous labs, are often integrated into a single circuit which performs some functions. One class of circuits, combinational circuits, can be found in almost every digital device and are therefore important to study. Here we look at how to design and implement combinational circuits.

Combinational Design Procedure:


	You have been learning boolean algebra and Karnaugh Maps in the class. 
	To acheive "Two-Level Minimum Cost Designs", Simplified SOP Form or 
	Simplified POS Form should be obtained by using Karnaugh Map Reduction.
	With these knowledge we have all the tools for combinational design. 
	The steps taken for a combinational design are as follows: 
	 Define/describe/state the problem
	
Determine the number of variables needed and 
assign letter symbols to the input and output variables
	
Construct the function table that defines the relationship 
between the inputs and outputs
	
Simplify the boolean expression for each output. 
This is done with Karnaugh Maps or Boolean algebra.
	
Draw the logic diagram and implement the test circuit

Karnaugh Map Reduction

As reductions using the theorems of Boolean algebra are at times tricky, a graphical method of carrying out function reductions was developed by M. Karnaugh which makes logic reduction much easier. The Karnaugh map is shown below for three and four variable functions.

The maps above are organized so that groups like AB + AB' can be recognized and reduced (to A in this case) visually. To do this the truth table is mapped into the Karnaugh map and then squares of '1's are circled from the biggest square to the smallest square. It is important that the minimum number of circles is used and that the biggest possible squares is used in order to achieve a minimum reduction. When identifying squares, it must be kept in mind that the maps are actually three dimensional as shown below:

Example of using Karnaugh map:

The truth table on the right has been mapped into the KMap and then the squares of '1 's circled. Notice that the number of '1's in a square is always a power of 2.

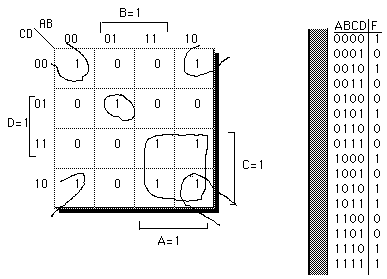
Writing out the term for each group yields the expression below: F = A'BC'D + AC + B'D'

Karnaugh Map Reduction Procedure

Procedure for getting the SOP form:

Mark '1' for those squares corresponding to the minterms of the function, mark the rest of squares with '0'.
Find all adjacent squares that correspond to prime implicants (the number of adjacent squares to be used is power of two)
and circle them together, write down their corresponding products.
Find the largest adjacent squares on the map, circle them together, and write down the corresponding products.
Repeat this step until all 1's have been circled.
List all products and write them in SOP form.
Note:
Any square marked by '1' can be selected more than once, but at least once.
If there are 2^k squares adjacent together, then k variables should be eliminated.

Example of a combinational design:

	
	
	and implement the test circuit

Assignments

Copyright: Department of Computer Science, University of Regina.

Colour Theme		Font Size Options