CS201 Lab: Design Adders & Subtractors
Objectives
- implement a half-adder as a sub-circuit
- implement a full adder using two half adders
- implement a half subtractor as a subcircuit
- use a half-adder to create a half-subtractors
- use two half subtractors or a full adder to implement a full subtractor
Review
When designing combinational circuits. We discussed five steps:
- Define/Describe/State the problem
- Determine the number of variables needed and assign letter symbols to the input and output variables
- Construct the function table that defines the relationship between the inputs and outputs
- Simplify the boolean expression for each output. This is done with Karnaugh Maps or Boolean algebra
- Draw the logic diagram and implement the circuit in Logisim
We will look at designing a combinational circuit for a Half-Adder.
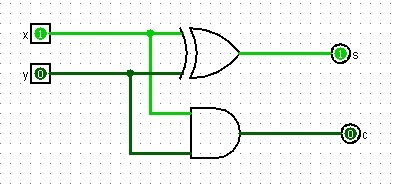
Half-Adder
1. State the Problem:
- A Half-adder is a combinational circuit that performs the addition of 2 bits.
- The results of the Half-adder are a sum and carry bit.
- Examples (remember, what is 10 in binary?):
0 + 0 = 00 where sum = 0, carry = 0 0 + 1 = 01 where sum = 1, carry = 0 1 + 0 = 01 where sum = 1, carry = 0 1 + 1 = 10 where sum = 0, carry = 1
2. Assign Variables:
- Inputs: 2 bits (x and y)
- Outputs: 2 bits (s and c)
3. Construct the Function Table:
You should be able to fill in the boxes for c and s:
Input |
Output |
|||
x |
y |
c |
s |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
|
4. Simplify
Here is where we cheat a little. We will not use the Karnaugh maps. Because you have a simple truth table (4 rows), you can match the gates with the gates you already know.
Here are the truth tables for the gates you know:
| x | y | AND | NAND | NOR | OR | XOR |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 |
- Which gate will c use?
- Which gate will s use?
We can get the following expressions by observation. There are two inputs, two gates, and two outputs.
s = x XOR y
c = xy
5. Draw the Logic Diagram and implement it in Logisim
You can draw circuits from the above expressions.
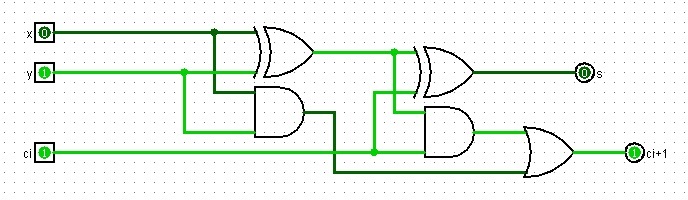
Full-Adder
You can now try and use two half-adders to create a full adder. Again, we will break the problem into steps:
1. State the Problem:
- A Full-adder is a combinational circuit that forms the arithmetic sum of 3 input bits (one is a carry bit).
- The results of the Full-adder are a sum and carry bit.
- Examples (remember, what is 11 in binary?):
0 + 1 + 0 = 01 where carry = 0, sum = 1, 0 + 0 + 1 = 01 where carry = 0, sum = 1, 1 + 0 + 1 = 10 where carry = 1, sum = 0, 1 + 1 + 1 = 11 where carry = 1, sum = 1,
2. Assign Variables:
- Inputs: 3 bits (x, y and ci)
- Outputs: 2 bits (s and ci+1)
3. Construct the Function Table:
Fill in the truth table with what you think ci+1 and s should be. A few have already been filled in for you.
Input |
Output |
||||
x |
y |
ci |
ci+1 |
s |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
|
4. Simplify
You can use the Karnaugh Map reduction method to find the simplfied expressions and then draw the full adder circuit.
Here are the functions for your convenience.
s = x XOR y XOR ci ci+1 = xy + ci(x XOR y)
5. Draw Logic Circuit
You can draw circuits from these expressions and find that a full adder can be designed by using two "Half Adders" and one additional OR gate.