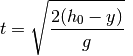Arrays
Arrays are used to store multiple values in one single variable. The array is called the NumPy array. NumPy (Numerical Python) is an open source Python library that is used in almost every field of science and engineering. It contains a multi-dimensional array and matrix data structures. NumPy can be used to perform a wide variety of mathematical operations on arrays. It is formally called ndarray. The elements of a NumPy array are usually numbers, strings, or other objects. When the elements are numbers, they must all be of the same type. For example, they might be all integers or all floating point numbers.
https://www.w3schools.com/python/python_arrays.asp
To access NumPy and its functions, import it in your Python code like this:
import numpy as np
This is widely adopted standard we should all follow. https://numpy.org/doc/stable/user/absolute_beginners.html
Differences between lists and arrays
They are a few differences between lists and arrays.
-
- Lists are part of the core Python programming language, you do not need to import any packages.
- Arrays are a part of the numerical computing package NumPy. In order to use arrays, you have to import NumPy package.
- Types of elements
- List elements can be different types.
- Array elements must all be of the same type.
- Arrays allow Boolean indexing; lists do not. See section 3.3.4.2 in the following link https://physics.nyu.edu/pine/pymanual/html/chap3/chap3_arrays.html#numpy-arrays
- Arrays support element-by-element addition and multiplication.
More websites on the differences between Python lists and arrays
https://www.geeksforgeeks.org/difference-between-list-and-array-in-python/ https://www.pythoncentral.io/the-difference-between-a-list-and-an-array/Creating arrays
NumPy has several functions for creating arrays. The first one is the array function, which converts a list to an array.
We can use Lists as arrays. To work with arrays in Python, import NumPy is required.
The following examples are from https://physics.nyu.edu/pine/pymanual/html/chap3/chap3_arrays.html#numpy-arrays
The array function
Converts a list to an array. You can try the following code in any Python console directly.In [1]: a = [0, 3, 5, 90, 123] In [2]: import numpy as np In [3]: b = np.array(a) In [4]: b Out[4]: array([0, 3, 5, 90, 123]) In [5]: c = np.array([1, 4., -2, 7]) In [6]: c Out[6]: array([ 1., 4., -2., 7.])
b is an integer array since it was created from a list of integers. c is a floating point array even though only one of the elements of the list was a floating point number. The array function automatically promotes all of the numbers to the type of the most general entry in the list, which in this case is a floating point number. In the case that elements of the list is made up of numbers and strings, all the elements become strings when an array is formed from a list.
You can also write the above array program in replit or Spyder IDE editor:
#Program name: array_example.py
import numpy as np
def main():
a = [0, 3, 5, 90, 123]
print('Array a is: ', a)
b = np.array(a)
print('Array b is: ', b)
c = np.array([1, 4., -2, 7])
print('Array c is: ', c)
main()
https://physics.nyu.edu/pine/pymanual/html/chap3/chap3_arrays.html#numpy-arrays
The linspace or logspace function
The second way to create arrays is to use the NumPy linspace or logspace functions. The linspace function creates an array of N evenly spaced points between a starting point and an ending point. The form of the function is linspace(start, stop, N). If the third argument N is omitted, then N=50.
In [7]: np.linspace(0, 10, 5) Out[7]: array([ 0. , 2.5, 5. , 7.5, 10. ])
The linspace function produced 5 evenly spaced points between 0 and 10 inclusive.
NumPy has a function logspace that produces evenly spaced points on a logarithmically spaced scale. The arguments are the same as those for linspace except that start and stop refer to a power of 10.
In [8]: np.logspace(1, 3, 5) Out[8]: array([ 10. , 31.6, 100. , 316.2, 1000. ])
The arange function
The third way to create an array is the NumPy arange function. The form of the function is arange(start, stop, step). If the third argument is omitted step=1. If the first and third arguments are omitted, then start=0 and step=1.
In [9]: np.arange(0, 10, 2) Out[9]: array([0, 2, 4, 6, 8]) In [10]: np.arange(0., 10, 2) Out[10]: array([ 0., 2., 4., 6., 8.]) In [11]: np.arange(0, 10, 1.5) Out[11]: array([ 0. , 1.5, 3. , 4.5, 6. , 7.5, 9. ])
The arange function produces points evenly spaced between 0 and 10 exclusive of the final point. Notice that arange produces an integer array in the first case but a floating point array in the other two cases. In general, arange produces an integer array if the arguments are all integers; making any one of the arguments a float causes the array to be a float.
The zeros and ones functions
Zeros and ones functions create arrays where all the elements are either zeros or ones. They each take on mandatory argument, the number of elements in the array, and one optional argument that specifies the data type of the array. Left unspecified, the data type is a float. Here are three examples
In [12]: np.zeros(6) Out[12]: array([ 0., 0., 0., 0., 0., 0.]) In [13]: np.ones(8) Out[13]: array([ 1., 1., 1., 1., 1., 1., 1., 1.]) In [14]: ones(8, dtype=int) Out[14]: array([1, 1, 1, 1, 1, 1, 1, 1])
Mathematical operations with arrays
You can perform mathematical operations on arrays.
In [15]: import numpy as np
In [15]: a = np.linspace(-1., 5, 7)
In [16]: a
Out[16]: array([-1., 0., 1., 2., 3., 4., 5.])
In [17]: a*6
Out[17]: array([ -6., 0., 6., 12., 18., 24., 30.])
In [18]: a/5
Out[18]: array([-0.2, 0. , 0.2, 0.4, 0.6, 0.8, 1. ])
In [19]: a**3
Out[19]: array([ -1., 0., 1., 8., 27., 64., 125.])
In [20]: a+4
Out[20]: array([ 3., 4., 5., 6., 7., 8., 9.])
In [21]: a-10
Out[21]: array([-11., -10., -9., -8., -7., -6., -5.])
In [22]: (a+3)*2
Out[22]: array([ 4., 6., 8., 10., 12., 14., 16.])
In [23]: np.sin(a)
Out[23]: array([-0.84147098, 0. , 0.84147098, 0.90929743,
0.14112001, -0.7568025 , -0.95892427])
In [24]: np.exp(-a)
Out[24]: array([ 2.71828183, 1. , 0.36787944, 0.13533528,
0.04978707, 0.01831564, 0.00673795])
In [25]: 1. + np.exp(-a)
Out[25]: array([ 3.71828183, 2. , 1.36787944, 1.13533528,
1.04978707, 1.01831564, 1.00673795])
In [26]: b = 9*np.ones(8)
In [27]: b
Out[27]: array([9., 9., 9., 9., 9., 9., 9., 9.])
In [28] c = np.sqrt(b)
In [29]: c
Out[29]: array([3., 3., 3., 3., 3., 3., 3., 3.])
Slicing and addressing arrays
This example is modified from "Introduction to Python for Science and Engineering" by David Pine.
We have two arrays y and t for position vs. time of a falling object, say a ball, and we want to use these data to calculate the velocity as a function of time:
y = array([ 0. , 1.3, 5. , 10.9, 18.9, 28.7, 40. ]) t = array([ 0. , 0.49, 1. , 1.5 , 2.08, 2.55, 3.2 ])
the average velocity for time interval i by the formula
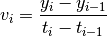
We can easily calculate the entire array of velocities using the slicing and vectorized subtraction properties of NumPy arrays by noting that we can create two y arrays displaced by one index.
y[:-1] array([ 0. , 1.3, 5. , 10.9, 18.9, 28.7]) y[1:] array([ 1.3, 5. , 10.9, 18.9, 28.7, 40. ])
The element-by-element difference of these two arrays is
y[1:]-y[:-1] array([ 1.3, 3.7, 5.9, 8. , 9.8, 11.3])
The element-by-element difference of the two arrays y[1:]-y[:-1] divided by t[1:]-t[:-1] gives the entire array of velocities.
Here is the Python program to calculate the average velocity by using the provided formula.
import numpy as np
def main():
y = np.array([0., 1.3, 5., 10.9, 18.9, 28.7, 40.])
t = np.array([0., 0.49, 1., 1.5, 2.08, 2.55, 3.2])
v = (y[1:]-y[:-1])/(t[1:]-t[:-1])
print("Velocity (v) is: ", v)
main()
 .
.